· Joseph · Online Course · 5 min read
Algorithm - hash map and set
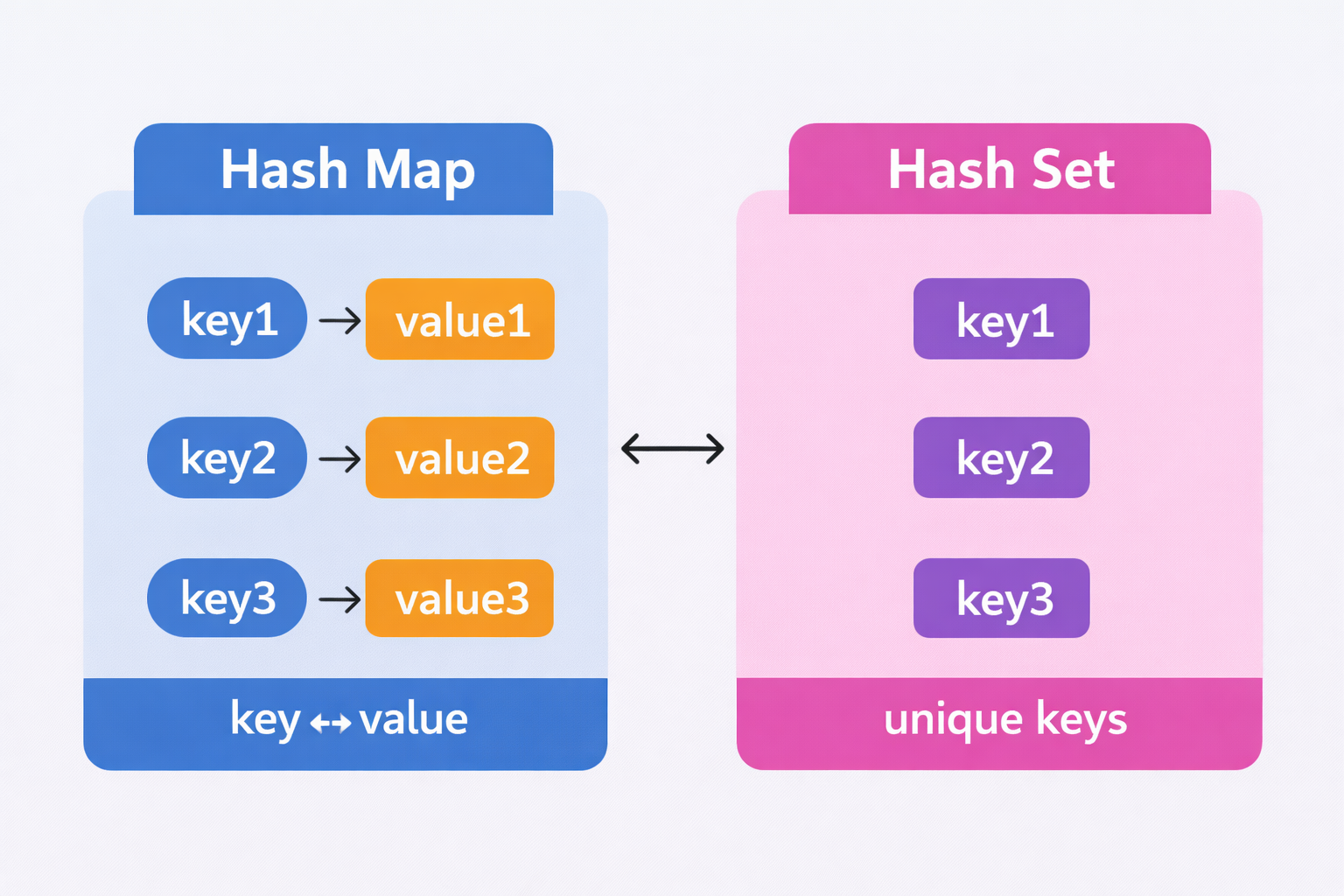
Set and Map 平常就有在用,map存的是Key-value pair、Set存的是unique value。而且操作上來說平均都是**O(1)**時間複雜度。這篇就來看看他們適合解哪些題型吧。
TOC
- Map vs. Set
- Pair Sum - Unsorted
- Verify Sudoku Board
- Zero Striping
- Longest Chain of Consecutive Numbers
- Geometric Sequence Triplets
- Conclusion
Map vs. Set
| 特性 | Hash Map(雜湊表 / 字典) | Hash Set(雜湊集合) |
|---|---|---|
| 核心概念 | Key–Value Pair的集合 | 唯一元素(Unique Keys)的集合 |
| 儲存內容 | 儲存 (Key, Value),Key 不可重複,Value 可重複 | 僅儲存 Key,且 Key 不可重複(自動去重) |
| 主要用途 | 當你需要建立「A 對應到 B」的關係時 例如:統計頻率、儲存原始索引 | 當你只需要知道「某物是否存在」或「去重」時 例如:判斷是否看過該數字、過濾重複名單 |
| 存取方式 | 透過 Key 來存取對應的 Valuemap.get(key) → value | 僅能查詢某元素 Key 是否存在set.contains(key) → true / false |
| 常見操作 | put(key, value)get(key)containsKey(key) | add(key)remove(key)contains(key) |
| 時間複雜度 | 新增 / 查詢 / 刪除:平均皆為 O(1) | 新增 / 查詢 / 刪除:平均皆為 O(1) |
| 程式語言範例 | Python:dict, {k: v} | Python:set, {k} |
Pair Sum - Unsorted
關鍵在於把data 當成 key、把index 當成 value,然後找每個data的補數(target - data)有沒有在map的key裡,有的話把補數的value抓出來,也就是補數的index了。
from typing import List
def pair_sum_unsorted(nums: List[int], target: int) -> List[int]:
# Write your code here
hash_map = {}
for i, x in enumerate(nums):
complementary = target - x
if complementary in hash_map:
return [hash_map[complementary], i]
hash_map[x] = i
return []Verify Sudoku Board
驗證sudoku board關鍵在
- row 要有9個set
- col 要有9個set
- 每個3x3 subgrid 都要有1個set,所以對3x3 subgrid共要有9個set
for-loop兩層去看每個[i][j] 的cell,其row-i, col-j 跟 subgrid-i-j 的 set有沒有重複的值。
from typing import List
def verify_sudoku_board(board: List[List[int]]) -> bool:
row_set = [set() for i in range(9)]
col_set = [set() for i in range(9)]
# i // 3 * 3 + j // 3
subgrid = [set() for i in range(9)]
for i in range(9):
for j in range(9):
num = board[i][j]
if num == 0:
continue
if num in row_set[i]:
return False
if num in col_set[j]:
return False
if num in subgrid[i // 3 * 3 + j // 3]:
return False
row_set[i].add(num)
col_set[j].add(num)
subgrid[i // 3 * 3 + j // 3].add(num)
return TrueZero Striping
Zero striping重點是要跑兩次nested loop (m * n),第一次要找出0所在的(i, j),分別存入row跟col的set。第二次loop就把 (i, j) 中如果i在row set或j在col set則把 (i, j) 設為 0
from typing import List
def zero_striping(matrix: List[List[int]]) -> None:
m = len(matrix)
if m == 0:
return
n = len(matrix[0])
if n == 0:
return
row_set = set()
col_set = set()
for i in range(m):
for j in range(n):
if matrix[i][j] == 0:
row_set.add(i)
col_set.add(j)
for i in range(m):
for j in range(n):
if j in col_set:
matrix[i][j] = 0
if i in row_set:
matrix[i][j] = 0
Longest Chain of Consecutive Numbers
這題我的解法跟ByteByteGo就不太一樣,影片是ByteByteGo的做法
我是跑2次loop,第1次找出head_set,然後第二次針對 head_set 每個去逐步 +1,找出最長的Consecutive Numbers
from typing import List
def longest_chain_of_consecutive_numbers(nums: List[int]) -> int:
chain_head_set = set()
for x in nums:
if not x - 1 in nums:
chain_head_set.add(x)
largest_chain = 0
for head in chain_head_set:
current = head
current_chain = 1
if current + 1 in nums:
while current + 1 in nums:
current += 1;
current_chain += 1
largest_chain = current_chain if current_chain > largest_chain else largest_chain
return largest_chainGeometric Sequence Triplets
這題的關鍵是出現的頻率相乘後相加,就是總共有幾個 Geometric Sequence Triplets。 但還有一個關鍵是,要找出 x/r, x, x*r 的組合。然後以x為current_value,計算出左邊map跟右邊map裡data的的頻率,才能相乘跟累加。
from typing import List
def geometric_sequence_triplets(nums: List[int], r: int) -> int:
left_hash = dict()
right_hash = dict()
for i in nums:
right_hash[i] = right_hash[i] + 1 if i in right_hash else 1
count = 0;
for i in nums:
if not i in left_hash:
left_hash[i] = 0
right_hash[i] -= 1
if i % r == 0:
count += left_hash.get(i / r, 0) * right_hash.get(i * r, 0)
left_hash[i] += 1
return count
Conclusion
以前都沒想過可以用Set跟Map去解題,都把它當成很單純的資料結構在存。現在知道針對這些頻率、重複、或需要 key-value pair做應用的,都可以用Set or Map去處理。
If you like this post, please connect with me on LinkedIn and give me some encouragement. Thanks.